Страница 120, часть 1 - гдз по алгебре 11 класс учебник часть 1, 2 Мордкович, Семенов

Авторы: Мордкович А. Г., Семенов П. В.
Тип: Учебник
Издательство: Мнемозина
Год издания: 2019 - 2025
Уровень обучения: базовый и углублённый
Часть: 1
Допущено Министерством просвещения Российской Федерации
Математика: алгебра и начала математического анализа
Популярные ГДЗ в 11 классе
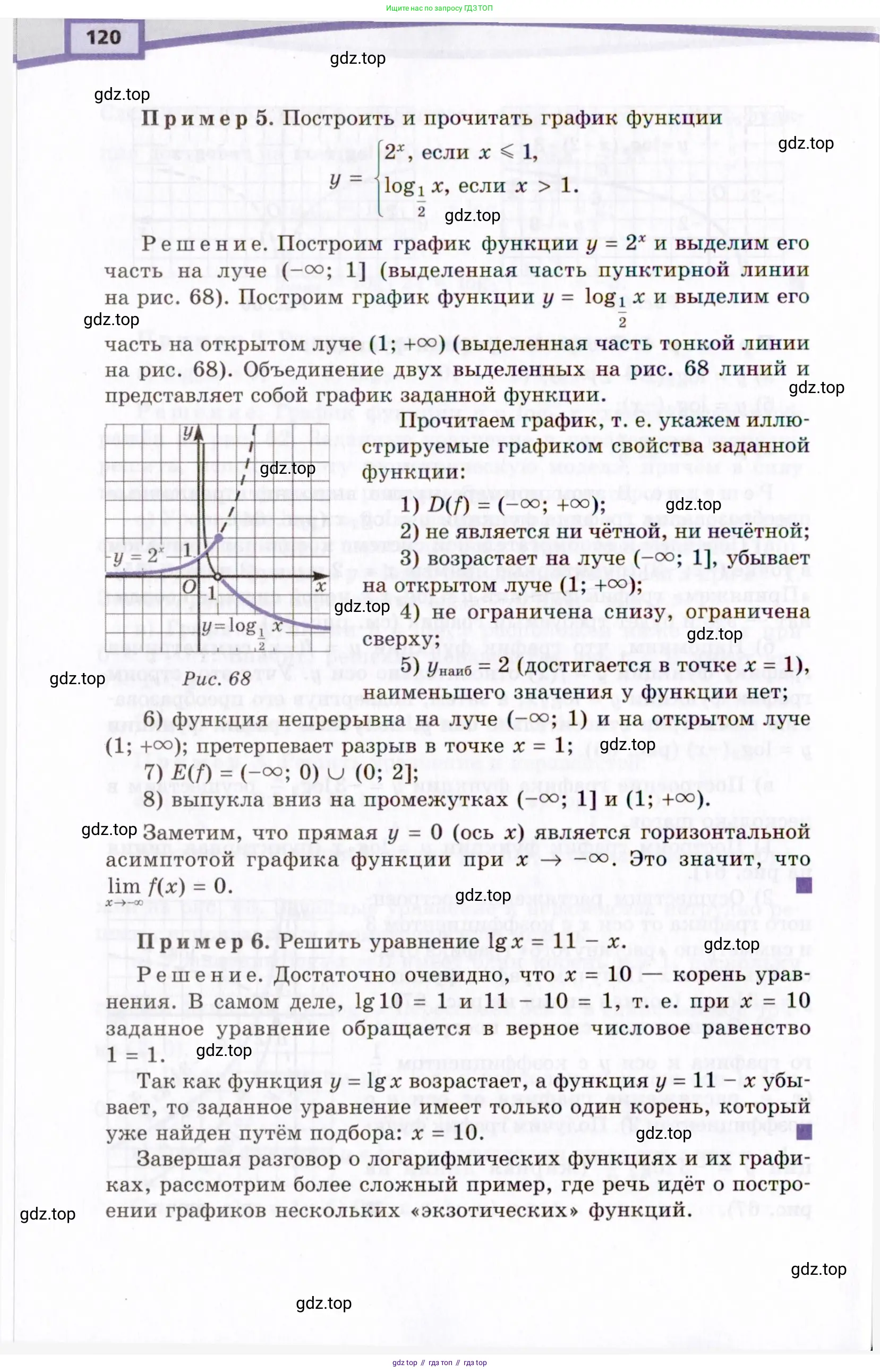
Часть 1. Cтраница 120
Другие страницы:
Помогло решение? Оставьте отзыв в комментариях ниже.
















