Номер 1.82, страница 35 - гдз по алгебре 10 класс учебник Никольский, Потапов

1.7*. Доказательство числовых неравенств. § 1. Действительные числа. Глава I. Корни, степени, логарифмы - номер 1.82, страница 35.

1.82* Докажите, что для любого натурального числа n справедливо неравенство:

a) $\frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \frac{1}{3 \cdot 4} + \dots + \frac{1}{n \cdot (n+1)} < 1;$

б) $\frac{1}{4 \cdot 5} + \frac{1}{5 \cdot 6} + \frac{1}{6 \cdot 7} + \dots + \frac{1}{(n+3) \cdot (n+4)} < \frac{1}{4};$

в) $\frac{1}{1 \cdot 5} + \frac{1}{5 \cdot 9} + \frac{1}{9 \cdot 13} + \dots + \frac{1}{(4n-3) \cdot (4n+1)} < \frac{1}{4};$

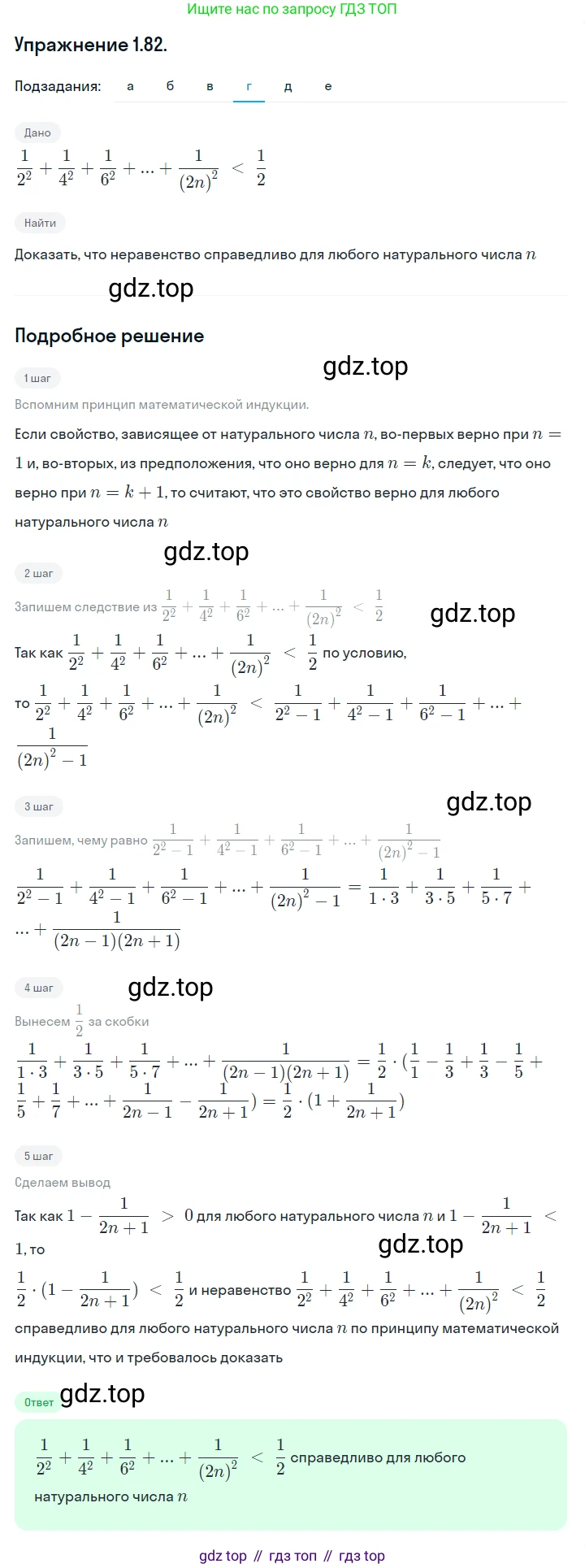
г) $\frac{1}{2^2} + \frac{1}{4^2} + \frac{1}{6^2} + \dots + \frac{1}{(2n)^2} < \frac{1}{2};$

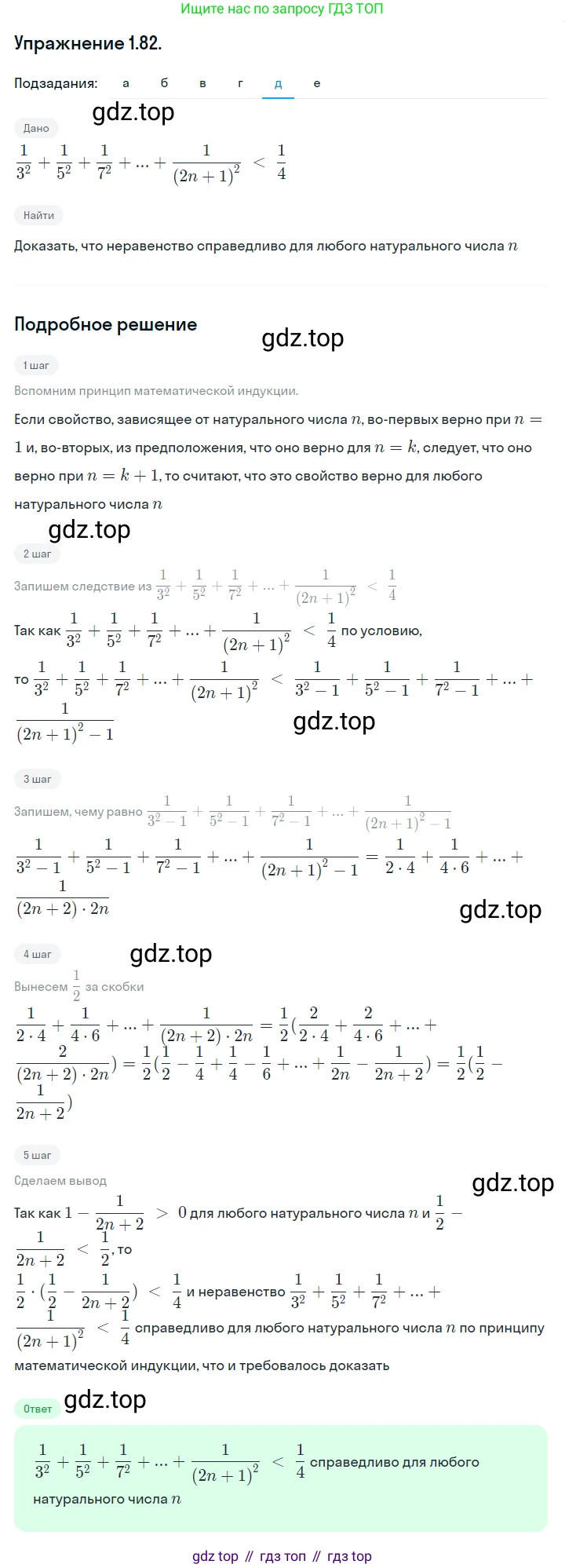
д) $\frac{1}{3^2} + \frac{1}{5^2} + \frac{1}{7^2} + \dots + \frac{1}{(2n+1)^2} < \frac{1}{4};$

е) $\frac{2}{(n+2)^2} < \frac{1}{n+1} - \frac{1}{n+3}.$

а)

Рассмотрим сумму $S_n = \frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \frac{1}{3 \cdot 4} + \dots + \frac{1}{n(n+1)}$.

Каждый член этой суммы можно представить в виде разности двух дробей, используя метод разложения на простейшие дроби:

$\frac{1}{k(k+1)} = \frac{1}{k} - \frac{1}{k+1}$

Таким образом, сумма является телескопической, так как промежуточные члены взаимно сокращаются:

$S_n = \sum_{k=1}^{n} (\frac{1}{k} - \frac{1}{k+1}) = (\frac{1}{1} - \frac{1}{2}) + (\frac{1}{2} - \frac{1}{3}) + (\frac{1}{3} - \frac{1}{4}) + \dots + (\frac{1}{n} - \frac{1}{n+1})$

В результате сокращения остаются только первый и последний члены:

$S_n = 1 - \frac{1}{n+1}$

Теперь докажем требуемое неравенство $S_n < 1$:

$1 - \frac{1}{n+1} < 1$

Поскольку $n$ — натуральное число ($n \ge 1$), то $n+1 \ge 2$, и, следовательно, дробь $\frac{1}{n+1}$ является положительным числом. Вычитание положительного числа из единицы дает результат, который строго меньше единицы. Неравенство справедливо для любого натурального $n$.

Ответ: Неравенство доказано.

б)

Рассмотрим сумму $S_n = \frac{1}{4 \cdot 5} + \frac{1}{5 \cdot 6} + \frac{1}{6 \cdot 7} + \dots + \frac{1}{(n+3)(n+4)}$.

Как и в предыдущем пункте, общий член ряда можно представить в виде разности:

$\frac{1}{(k+3)(k+4)} = \frac{1}{k+3} - \frac{1}{k+4}$

Сумма является телескопической. Запишем ее в развернутом виде, чтобы увидеть сокращения:

$S_n = \sum_{k=1}^{n} (\frac{1}{k+3} - \frac{1}{k+4}) = (\frac{1}{4} - \frac{1}{5}) + (\frac{1}{5} - \frac{1}{6}) + (\frac{1}{6} - \frac{1}{7}) + \dots + (\frac{1}{n+3} - \frac{1}{n+4})$

После сокращения промежуточных членов получаем:

$S_n = \frac{1}{4} - \frac{1}{n+4}$

Докажем неравенство $S_n < \frac{1}{4}$:

$\frac{1}{4} - \frac{1}{n+4} < \frac{1}{4}$

Так как $n$ — натуральное число ($n \ge 1$), то $n+4 \ge 5$, и дробь $\frac{1}{n+4}$ положительна. Вычитание положительного числа из $\frac{1}{4}$ дает результат, строго меньший $\frac{1}{4}$. Неравенство справедливо.

Ответ: Неравенство доказано.

в)

Рассмотрим сумму $S_n = \frac{1}{1 \cdot 5} + \frac{1}{5 \cdot 9} + \frac{1}{9 \cdot 13} + \dots + \frac{1}{(4n-3)(4n+1)}$.

Разложим общий член ряда на простейшие дроби:

$\frac{1}{(4k-3)(4k+1)} = \frac{1}{4} \left( \frac{1}{4k-3} - \frac{1}{4k+1} \right)$

Теперь сумма принимает вид:

$S_n = \sum_{k=1}^{n} \frac{1}{4} \left( \frac{1}{4k-3} - \frac{1}{4k+1} \right) = \frac{1}{4} \sum_{k=1}^{n} \left( \frac{1}{4k-3} - \frac{1}{4k+1} \right)$

Это телескопическая сумма:

$S_n = \frac{1}{4} \left[ (\frac{1}{1} - \frac{1}{5}) + (\frac{1}{5} - \frac{1}{9}) + (\frac{1}{9} - \frac{1}{13}) + \dots + (\frac{1}{4n-3} - \frac{1}{4n+1}) \right]$

После сокращения получаем:

$S_n = \frac{1}{4} \left( 1 - \frac{1}{4n+1} \right)$

Докажем неравенство $S_n < \frac{1}{4}$:

$\frac{1}{4} \left( 1 - \frac{1}{4n+1} \right) < \frac{1}{4}$

Умножим обе части на 4 (так как 4 > 0, знак неравенства не меняется):

$1 - \frac{1}{4n+1} < 1$

Для натурального $n \ge 1$, выражение $4n+1 \ge 5$, поэтому $\frac{1}{4n+1} > 0$. Выражение $1 - \frac{1}{4n+1}$ всегда меньше 1. Неравенство справедливо.

Ответ: Неравенство доказано.

г)

Рассмотрим сумму $S_n = \frac{1}{2^2} + \frac{1}{4^2} + \frac{1}{6^2} + \dots + \frac{1}{(2n)^2}$.

Вынесем общий множитель $\frac{1}{2^2} = \frac{1}{4}$ за скобки:

$S_n = \frac{1}{(2 \cdot 1)^2} + \frac{1}{(2 \cdot 2)^2} + \frac{1}{(2 \cdot 3)^2} + \dots + \frac{1}{(2n)^2} = \frac{1}{4} \left( \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \dots + \frac{1}{n^2} \right)$

Оценим сумму в скобках. Для любого натурального $k \ge 2$ справедливо неравенство $k^2 > k^2 - k = k(k-1)$, откуда $\frac{1}{k^2} < \frac{1}{k(k-1)}$.

Заменим каждый член суммы (кроме первого) на большую величину:

$\sum_{k=1}^{n} \frac{1}{k^2} = 1 + \sum_{k=2}^{n} \frac{1}{k^2} < 1 + \sum_{k=2}^{n} \frac{1}{k(k-1)}$

Сумма $\sum_{k=2}^{n} \frac{1}{k(k-1)}$ является телескопической, так как $\frac{1}{k(k-1)} = \frac{1}{k-1} - \frac{1}{k}$.

$\sum_{k=2}^{n} (\frac{1}{k-1} - \frac{1}{k}) = (\frac{1}{1} - \frac{1}{2}) + (\frac{1}{2} - \frac{1}{3}) + \dots + (\frac{1}{n-1} - \frac{1}{n}) = 1 - \frac{1}{n}$

Следовательно, $\sum_{k=1}^{n} \frac{1}{k^2} < 1 + (1 - \frac{1}{n}) = 2 - \frac{1}{n}$.

Подставим эту оценку в выражение для $S_n$:

$S_n = \frac{1}{4} \left( \sum_{k=1}^{n} \frac{1}{k^2} \right) < \frac{1}{4} (2 - \frac{1}{n})$

Так как $n \ge 1$, то $\frac{1}{n} > 0$, и $2 - \frac{1}{n} < 2$. Таким образом:

$S_n < \frac{1}{4} \cdot 2 = \frac{1}{2}$

Неравенство доказано.

Ответ: Неравенство доказано.

д)

Рассмотрим сумму $S_n = \frac{1}{3^2} + \frac{1}{5^2} + \frac{1}{7^2} + \dots + \frac{1}{(2n+1)^2}$.

Для оценки суммы воспользуемся методом сравнения. Для любого целого числа $m > 1$ справедливо неравенство $m^2 > m^2 - 1 = (m-1)(m+1)$, откуда следует $\frac{1}{m^2} < \frac{1}{(m-1)(m+1)}$.

Применим это к общему члену нашей суммы $a_k = \frac{1}{(2k+1)^2}$, где $m = 2k+1$. Для $k \ge 1$ имеем $m \ge 3$.

$\frac{1}{(2k+1)^2} < \frac{1}{((2k+1)-1)((2k+1)+1)} = \frac{1}{(2k)(2k+2)} = \frac{1}{4k(k+1)}$

Тогда исходная сумма меньше, чем сумма этих больших дробей:

$S_n = \sum_{k=1}^{n} \frac{1}{(2k+1)^2} < \sum_{k=1}^{n} \frac{1}{4k(k+1)} = \frac{1}{4} \sum_{k=1}^{n} \frac{1}{k(k+1)}$

Сумма $\sum_{k=1}^{n} \frac{1}{k(k+1)}$ нам уже знакома из пункта а). Она равна $1 - \frac{1}{n+1}$.

Подставляем это значение:

$S_n < \frac{1}{4} \left( 1 - \frac{1}{n+1} \right)$

Так как $n \ge 1$, то $1 - \frac{1}{n+1} < 1$. Следовательно:

$S_n < \frac{1}{4} \cdot 1 = \frac{1}{4}$

Неравенство доказано.

Ответ: Неравенство доказано.

е)

Нужно доказать неравенство: $\frac{2}{(n+2)^2} < \frac{1}{n+1} - \frac{1}{n+3}$.

Преобразуем правую часть неравенства, приведя дроби к общему знаменателю:

$\frac{1}{n+1} - \frac{1}{n+3} = \frac{(n+3) - (n+1)}{(n+1)(n+3)} = \frac{2}{(n+1)(n+3)}$

Теперь неравенство принимает вид:

$\frac{2}{(n+2)^2} < \frac{2}{(n+1)(n+3)}$

Поскольку числители дробей равны и положительны, неравенство будет верным, если знаменатель левой дроби больше знаменателя правой дроби:

$(n+2)^2 > (n+1)(n+3)$

Раскроем скобки в обеих частях неравенства:

$n^2 + 4n + 4 > n^2 + 4n + 3$

Вычтем из обеих частей $n^2 + 4n$:

$4 > 3$

Мы получили верное числовое неравенство. Так как все преобразования были эквивалентными для натуральных $n$ (знаменатели всегда положительны), исходное неравенство также верно.

Ответ: Неравенство доказано.