Номер 159, страница 298 - гдз по алгебре 10-11 класс учебник Колмогоров, Абрамов

Глава 5. Задачи на повторение. Параграф 4. Уравнения, неравенства, системы уравнений и неравенств - номер 159, страница 298.

Условие.

Решите неравенства (159–162).

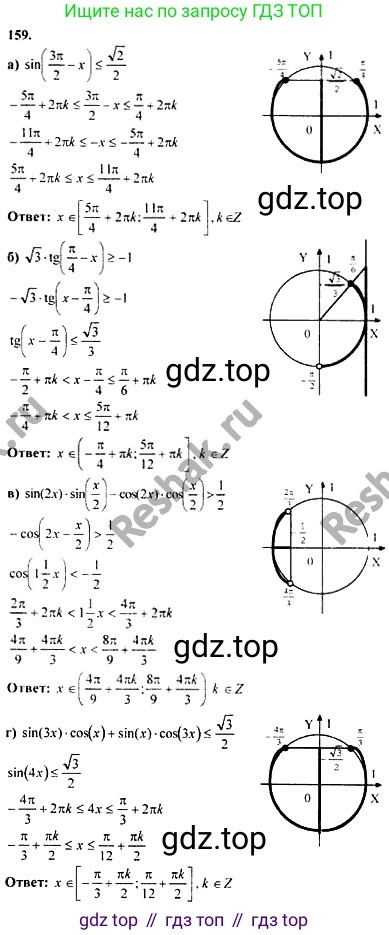
159. a) $sin(\\frac{3\\pi}{2} - x) \\le \\frac{\\sqrt{2}}{2};$

б) $\\sqrt{3} tg(\\frac{\\pi}{4} - x) \\ge -1;$

в) $sin 2x sin \\frac{x}{2} - cos 2x cos \\frac{x}{2} > \\frac{1}{2};$

г) $sin 3x cos x + sin x cos 3x \\le \\frac{\\sqrt{3}}{2}.$

Решение 1.

Решение 3.

Решение 5.

а)

Исходное неравенство: $sin(\frac{3\pi}{2} - x) \le \frac{\sqrt{2}}{2}$.

Для упрощения левой части неравенства применим формулу приведения $sin(\frac{3\pi}{2} - \alpha) = -cos(\alpha)$.

В результате неравенство принимает вид:

$-cos(x) \le \frac{\sqrt{2}}{2}$.

Умножим обе части неравенства на -1, изменив при этом знак неравенства на противоположный:

$cos(x) \ge -\frac{\sqrt{2}}{2}$.

Теперь решим это простейшее тригонометрическое неравенство. Найдём на единичной окружности все точки, абсцисса (косинус) которых больше или равна $-\frac{\sqrt{2}}{2}$.

Уравнение $cos(t) = -\frac{\sqrt{2}}{2}$ имеет решения $t = \pm\frac{3\pi}{4} + 2\pi k$, где $k \in \mathbb{Z}$.

Неравенству $cos(x) \ge -\frac{\sqrt{2}}{2}$ соответствуют значения $x$, принадлежащие дуге от $-\frac{3\pi}{4}$ до $\frac{3\pi}{4}$.

Таким образом, общее решение неравенства можно записать в виде двойного неравенства с учётом периодичности функции косинус:

$-\frac{3\pi}{4} + 2\pi k \le x \le \frac{3\pi}{4} + 2\pi k$, где $k \in \mathbb{Z}$.

Ответ: $-\frac{3\pi}{4} + 2\pi k \le x \le \frac{3\pi}{4} + 2\pi k$, $k \in \mathbb{Z}$.

б)

Исходное неравенство: $\sqrt{3} \ tg(\frac{\pi}{4} - x) \ge -1$.

Разделим обе части неравенства на $\sqrt{3}$:

$tg(\frac{\pi}{4} - x) \ge -\frac{1}{\sqrt{3}}$.

Воспользуемся свойством нечётности тангенса: $tg(-a) = -tg(a)$. Тогда $tg(\frac{\pi}{4} - x) = tg(-(x - \frac{\pi}{4})) = -tg(x - \frac{\pi}{4})$.

Неравенство переписывается в виде:

$-tg(x - \frac{\pi}{4}) \ge -\frac{1}{\sqrt{3}}$.

Умножим на -1, меняя знак неравенства:

$tg(x - \frac{\pi}{4}) \le \frac{1}{\sqrt{3}}$.

Сделаем замену $t = x - \frac{\pi}{4}$, чтобы получить простейшее неравенство: $tg(t) \le \frac{1}{\sqrt{3}}$.

Найдём решение для $t$ на основном интервале $(-\frac{\pi}{2}, \frac{\pi}{2})$. Уравнение $tg(t) = \frac{1}{\sqrt{3}}$ имеет решение $t = \frac{\pi}{6}$. Так как тангенс — возрастающая функция, неравенство $tg(t) \le \frac{1}{\sqrt{3}}$ выполняется при $-\frac{\pi}{2} < t \le \frac{\pi}{6}$.

Общее решение для $t$ с учётом периода тангенса, равного $\pi$:

$-\frac{\pi}{2} + \pi k < t \le \frac{\pi}{6} + \pi k$, где $k \in \mathbb{Z}$.

Выполним обратную замену $t = x - \frac{\pi}{4}$:

$-\frac{\pi}{2} + \pi k < x - \frac{\pi}{4} \le \frac{\pi}{6} + \pi k$.

Прибавим $\frac{\pi}{4}$ ко всем частям неравенства:

$-\frac{\pi}{2} + \frac{\pi}{4} + \pi k < x \le \frac{\pi}{6} + \frac{\pi}{4} + \pi k$.

Упростим выражения:

$-\frac{\pi}{4} + \pi k < x \le \frac{2\pi+3\pi}{12} + \pi k$.

$-\frac{\pi}{4} + \pi k < x \le \frac{5\pi}{12} + \pi k$, где $k \in \mathbb{Z}$.

Ответ: $-\frac{\pi}{4} + \pi k < x \le \frac{5\pi}{12} + \pi k$, $k \in \mathbb{Z}$.

в)

Исходное неравенство: $sin(2x) sin(\frac{x}{2}) - cos(2x) cos(\frac{x}{2}) > \frac{1}{2}$.

Вынесем знак минус за скобки в левой части:

$-(cos(2x) cos(\frac{x}{2}) - sin(2x) sin(\frac{x}{2})) > \frac{1}{2}$.

Выражение в скобках соответствует формуле косинуса суммы: $cos(\alpha + \beta) = cos(\alpha)cos(\beta) - sin(\alpha)sin(\beta)$.

Применим эту формулу для $\alpha = 2x$ и $\beta = \frac{x}{2}$:

$-cos(2x + \frac{x}{2}) > \frac{1}{2}$.

$-cos(\frac{5x}{2}) > \frac{1}{2}$.

Умножим обе части на -1, изменив знак неравенства:

$cos(\frac{5x}{2}) < -\frac{1}{2}$.

Сделаем замену $t = \frac{5x}{2}$. Неравенство примет вид $cos(t) < -\frac{1}{2}$.

На единичной окружности этому неравенству соответствуют точки, абсцисса которых меньше $-\frac{1}{2}$. Это дуга, расположенная между точками, соответствующими углам $\frac{2\pi}{3}$ и $\frac{4\pi}{3}$.

Таким образом, решение для $t$ в пределах одного оборота: $\frac{2\pi}{3} < t < \frac{4\pi}{3}$.

Общее решение для $t$ с учётом периодичности:

$\frac{2\pi}{3} + 2\pi k < t < \frac{4\pi}{3} + 2\pi k$, где $k \in \mathbb{Z}$.

Произведём обратную замену $t = \frac{5x}{2}$:

$\frac{2\pi}{3} + 2\pi k < \frac{5x}{2} < \frac{4\pi}{3} + 2\pi k$.

Умножим все части неравенства на $\frac{2}{5}$, чтобы выразить $x$:

$\frac{2}{5} \cdot \frac{2\pi}{3} + \frac{2}{5} \cdot 2\pi k < x < \frac{2}{5} \cdot \frac{4\pi}{3} + \frac{2}{5} \cdot 2\pi k$.

$\frac{4\pi}{15} + \frac{4\pi k}{5} < x < \frac{8\pi}{15} + \frac{4\pi k}{5}$, где $k \in \mathbb{Z}$.

Ответ: $\frac{4\pi}{15} + \frac{4\pi k}{5} < x < \frac{8\pi}{15} + \frac{4\pi k}{5}$, $k \in \mathbb{Z}$.

г)

Исходное неравенство: $sin(3x) cos(x) + sin(x) cos(3x) \le \frac{\sqrt{3}}{2}$.

Левая часть неравенства представляет собой формулу синуса суммы: $sin(\alpha + \beta) = sin(\alpha)cos(\beta) + cos(\alpha)sin(\beta)$.

Применив эту формулу для $\alpha = 3x$ и $\beta = x$, получим:

$sin(3x + x) \le \frac{\sqrt{3}}{2}$.

$sin(4x) \le \frac{\sqrt{3}}{2}$.

Введём замену $t = 4x$, чтобы получить простейшее неравенство: $sin(t) \le \frac{\sqrt{3}}{2}$.

Решим его с помощью единичной окружности. Нам нужны точки, ордината (синус) которых не превышает $\frac{\sqrt{3}}{2}$.

Уравнение $sin(t) = \frac{\sqrt{3}}{2}$ имеет решения $t = \frac{\pi}{3} + 2\pi k$ и $t = \frac{2\pi}{3} + 2\pi k$.

Неравенство выполняется для всех точек на окружности, кроме дуги между $\frac{\pi}{3}$ и $\frac{2\pi}{3}$.

Решение можно записать как единый интервал, например, от $\frac{2\pi}{3}$ до $\frac{\pi}{3}$ следующего оборота ($ \frac{\pi}{3}+2\pi = \frac{7\pi}{3} $). Другой, более удобный способ записи — использовать отрицательные углы: решение соответствует дуге от $-\frac{4\pi}{3}$ до $\frac{\pi}{3}$.

Общее решение для $t$:

$-\frac{4\pi}{3} + 2\pi k \le t \le \frac{\pi}{3} + 2\pi k$, где $k \in \mathbb{Z}$.

Выполним обратную замену $t = 4x$:

$-\frac{4\pi}{3} + 2\pi k \le 4x \le \frac{\pi}{3} + 2\pi k$.

Разделим все части неравенства на 4:

$-\frac{4\pi}{12} + \frac{2\pi k}{4} \le x \le \frac{\pi}{12} + \frac{2\pi k}{4}$.

$-\frac{\pi}{3} + \frac{\pi k}{2} \le x \le \frac{\pi}{12} + \frac{\pi k}{2}$, где $k \in \mathbb{Z}$.

Ответ: $-\frac{\pi}{3} + \frac{\pi k}{2} \le x \le \frac{\pi}{12} + \frac{\pi k}{2}$, $k \in \mathbb{Z}$.