Номер 120, страница 327 - гдз по алгебре 10-11 класс учебник Колмогоров, Абрамов

Глава 6. Задачи повышенной трудности. Параграф 3. Уравнения, неравенства и системы - номер 120, страница 327.

Условие.

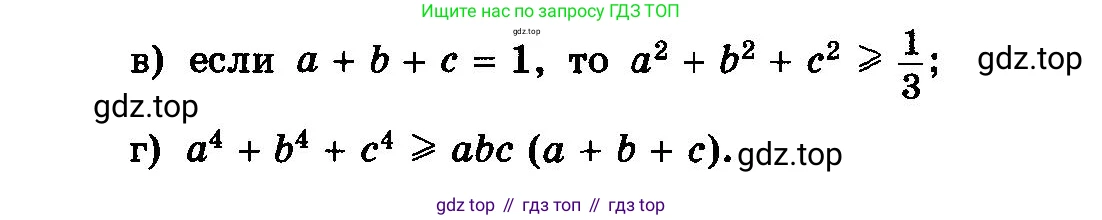
Докажите неравенства (120–124).

120.а) $a^2 + b^2 + c^2 \ge ab + ac + bc;$

б) $(a + b) (b + c) (c + a) \ge 8abc (a \ge 0, b \ge 0, c \ge 0);$

в) если $a + b + c = 1$, то $a^2 + b^2 + c^2 \ge \frac{1}{3};$

г) $a^4 + b^4 + c^4 \ge abc (a + b + c).$

Решение 3.

Решение 5.

а) $a^2 + b^2 + c^2 \ge ab + ac + bc$

Для доказательства перенесем все члены неравенства в левую часть:

$a^2 + b^2 + c^2 - ab - ac - bc \ge 0$

Умножим обе части неравенства на 2. Так как 2 > 0, знак неравенства не изменится:

$2a^2 + 2b^2 + 2c^2 - 2ab - 2ac - 2bc \ge 0$

Сгруппируем члены таким образом, чтобы можно было выделить полные квадраты разностей:

$(a^2 - 2ab + b^2) + (a^2 - 2ac + c^2) + (b^2 - 2bc + c^2) \ge 0$

Запишем сгруппированные члены в виде квадратов:

$(a - b)^2 + (a - c)^2 + (b - c)^2 \ge 0$

Квадрат любого действительного числа является неотрицательной величиной. Следовательно, $(a - b)^2 \ge 0$, $(a - c)^2 \ge 0$ и $(b - c)^2 \ge 0$. Сумма неотрицательных чисел также неотрицательна. Таким образом, последнее неравенство верно для любых действительных чисел $a, b, c$. Поскольку все преобразования были равносильными, исходное неравенство также верно. Равенство достигается, когда все слагаемые равны нулю, то есть когда $a - b = 0$, $a - c = 0$ и $b - c = 0$, что эквивалентно условию $a = b = c$.

Ответ: Неравенство $a^2 + b^2 + c^2 \ge ab + ac + bc$ доказано.

б) $(a + b)(b + c)(c + a) \ge 8abc$ (при $a \ge 0, b \ge 0, c \ge 0$)

Для доказательства этого неравенства воспользуемся неравенством о среднем арифметическом и среднем геометрическом (неравенство Коши) для двух неотрицательных чисел: $\frac{x+y}{2} \ge \sqrt{xy}$, или $x+y \ge 2\sqrt{xy}$.

Применим это неравенство для пар неотрицательных чисел $(a, b)$, $(b, c)$ и $(c, a)$:

$a + b \ge 2\sqrt{ab}$

$b + c \ge 2\sqrt{bc}$

$c + a \ge 2\sqrt{ca}$

Поскольку все части этих неравенств неотрицательны (так как $a, b, c \ge 0$), мы можем их перемножить, при этом знак неравенства сохранится:

$(a + b)(b + c)(c + a) \ge (2\sqrt{ab})(2\sqrt{bc})(2\sqrt{ca})$

Упростим правую часть полученного неравенства:

$8\sqrt{ab \cdot bc \cdot ca} = 8\sqrt{a^2 b^2 c^2} = 8\sqrt{(abc)^2}$

Так как $a, b, c \ge 0$, то $abc \ge 0$, и следовательно, $\sqrt{(abc)^2} = abc$.

Таким образом, мы получаем искомое неравенство:

$(a + b)(b + c)(c + a) \ge 8abc$

Равенство достигается, когда во всех трех примененных неравенствах Коши достигается равенство, то есть когда $a = b$, $b = c$ и $c = a$, что означает $a = b = c$.

Ответ: Неравенство $(a + b)(b + c)(c + a) \ge 8abc$ для $a \ge 0, b \ge 0, c \ge 0$ доказано.

в) если $a + b + c = 1$, то $a^2 + b^2 + c^2 \ge \frac{1}{3}$

Для доказательства воспользуемся результатом, полученным в пункте а): $a^2 + b^2 + c^2 \ge ab + ac + bc$.

Рассмотрим известную формулу квадрата суммы трех чисел:

$(a + b + c)^2 = a^2 + b^2 + c^2 + 2(ab + ac + bc)$

Из неравенства пункта а) следует, что $ab + ac + bc \le a^2 + b^2 + c^2$. Используя это, мы можем оценить правую часть формулы квадрата суммы сверху:

$(a + b + c)^2 = a^2 + b^2 + c^2 + 2(ab + ac + bc) \le (a^2 + b^2 + c^2) + 2(a^2 + b^2 + c^2)$

$(a + b + c)^2 \le 3(a^2 + b^2 + c^2)$

По условию задачи $a + b + c = 1$. Подставим это значение:

$1^2 \le 3(a^2 + b^2 + c^2)$

$1 \le 3(a^2 + b^2 + c^2)$

Разделив обе части на 3, получим искомое неравенство:

$a^2 + b^2 + c^2 \ge \frac{1}{3}$

Равенство достигается, когда $ab + ac + bc = a^2 + b^2 + c^2$, что, как показано в пункте а), происходит при $a = b = c$. Учитывая условие $a + b + c = 1$, получаем $a = b = c = \frac{1}{3}$.

Ответ: Утверждение "если $a + b + c = 1$, то $a^2 + b^2 + c^2 \ge \frac{1}{3}$" доказано.

г) $a^4 + b^4 + c^4 \ge abc(a + b + c)$

Для доказательства этого неравенства мы дважды применим неравенство из пункта а): $x^2 + y^2 + z^2 \ge xy + yz + zx$.

Шаг 1: Применим это неравенство для $x = a^2, y = b^2, z = c^2$.

$(a^2)^2 + (b^2)^2 + (c^2)^2 \ge a^2b^2 + b^2c^2 + c^2a^2$

$a^4 + b^4 + c^4 \ge a^2b^2 + b^2c^2 + c^2a^2$

Шаг 2: Теперь докажем, что $a^2b^2 + b^2c^2 + c^2a^2 \ge abc(a + b + c)$. Для этого снова применим неравенство из пункта а), но для переменных $x = ab, y = bc, z = ca$.

$(ab)^2 + (bc)^2 + (ca)^2 \ge (ab)(bc) + (bc)(ca) + (ca)(ab)$

$a^2b^2 + b^2c^2 + c^2a^2 \ge ab^2c + abc^2 + a^2bc$

Вынесем общий множитель $abc$ в правой части:

$a^2b^2 + b^2c^2 + c^2a^2 \ge abc(b + c + a)$

Шаг 3: Объединим результаты. Из шага 1 мы имеем $a^4 + b^4 + c^4 \ge a^2b^2 + b^2c^2 + c^2a^2$. Из шага 2 мы имеем $a^2b^2 + b^2c^2 + c^2a^2 \ge abc(a + b + c)$. Используя свойство транзитивности для неравенств, получаем:

$a^4 + b^4 + c^4 \ge a^2b^2 + b^2c^2 + c^2a^2 \ge abc(a + b + c)$

Следовательно, $a^4 + b^4 + c^4 \ge abc(a + b + c)$.

Равенство достигается, когда в обоих примененных неравенствах достигается равенство. Для первого неравенства это $a^2 = b^2 = c^2$. Для второго — $ab = bc = ca$. Совместное выполнение этих условий для действительных чисел возможно тогда и только тогда, когда $a = b = c$.

Ответ: Неравенство $a^4 + b^4 + c^4 \ge abc(a + b + c)$ доказано.