Номер 858, страница 219 - гдз по геометрии 10-11 класс учебник Атанасян, Бутузов

Авторы: Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Киселёва Л. С.
Тип: Учебник
Издательство: Просвещение
Год издания: 2019 - 2025
Уровень обучения: базовый и углублённый
Цвет обложки: коричневый с ромбами
ISBN: 978-5-09-103606-0 (2023)
Допущено Министерством просвещения Российской Федерации
Математика: алгебра и начала математического анализа, геометрия
Популярные ГДЗ в 10 классе
Глава 8. Некоторые сведения из планиметрии. Параграф 3. Теоремы Менелая и Чевы - номер 858, страница 219.
№858 (с. 219)
Условие. №858 (с. 219)
скриншот условия

858. Треугольники АВС и А₁В₁С₁ расположены так, что прямые АВ и А₁В₁, ВС и В₁С₁, СА и С₁А₁ пересекаются в точках Р, Q, R. Докажите, что прямые АА₁, ВВ₁ и СС₁ пересекаются в одной точке или попарно параллельны тогда и только тогда, когда точки Р, Q и R лежат на одной прямой (теорема Дезарга).
Решение 2. №858 (с. 219)
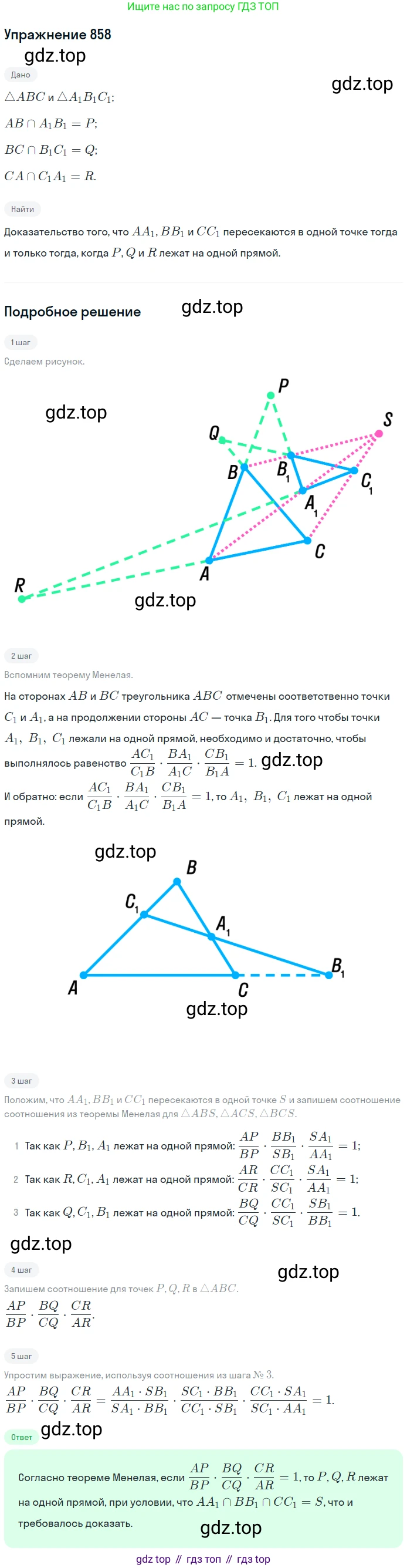
Решение 6. №858 (с. 219)
Теорема Дезарга является фундаментальным результатом проективной геометрии и утверждает эквивалентность двух условий: центральной и осевой перспективности двух треугольников. Доказательство состоит из двух частей, так как это утверждение типа "тогда и только тогда".
Пусть даны два треугольника $ABC$ и $A_1B_1C_1$.Точки пересечения соответственных сторон: $P = AB \cap A_1B_1$, $Q = BC \cap B_1C_1$, $R = CA \cap C_1A_1$.Прямые, соединяющие соответственные вершины: $AA_1, BB_1, CC_1$.
Условие 1 (центральная перспективность): Прямые $AA_1, BB_1, CC_1$ пересекаются в одной точке (центр перспективы) или попарно параллельны.
Условие 2 (осевая перспективность): Точки $P, Q, R$ лежат на одной прямой (ось перспективы).
Теорема утверждает, что Условие 1 выполняется тогда и только тогда, когда выполняется Условие 2.
Доказательство необходимости (Условие 1 $\implies$ Условие 2)
Предположим, что прямые $AA_1, BB_1, CC_1$ пересекаются в одной точке или параллельны. Нам нужно доказать, что точки $P, Q, R$ лежат на одной прямой.
Случай 1: Прямые $AA_1, BB_1, CC_1$ пересекаются в точке $O$.
Мы используем теорему Менелая. Рассмотрим треугольник $OAB$ и прямую $A_1B_1P$, которая пересекает его стороны (или их продолжения) в точках $A_1, B_1, P$. По теореме Менелая для $\triangle OAB$ и секущей $A_1B_1P$:
$\frac{OA_1}{A_1A} \cdot \frac{AP}{PB} \cdot \frac{BB_1}{B_1O} = 1$
Отсюда выразим отношение $\frac{AP}{PB}$:$\frac{AP}{PB} = \frac{A_1A}{OA_1} \cdot \frac{B_1O}{BB_1}$
Аналогично, применим теорему Менелая к $\triangle OBC$ и секущей $B_1C_1Q$:
$\frac{OB_1}{B_1B} \cdot \frac{BQ}{QC} \cdot \frac{CC_1}{C_1O} = 1$
Отсюда: $\frac{BQ}{QC} = \frac{B_1B}{OB_1} \cdot \frac{C_1O}{CC_1}$
И к $\triangle OCA$ и секущей $C_1A_1R$:
$\frac{OC_1}{C_1C} \cdot \frac{CR}{RA} \cdot \frac{AA_1}{A_1O} = 1$
Отсюда: $\frac{CR}{RA} = \frac{C_1C}{OC_1} \cdot \frac{A_1O}{AA_1}$
Теперь, чтобы доказать, что точки $P, Q, R$ лежат на одной прямой, мы используем обратную теорему Менелая для $\triangle ABC$. Нам нужно показать, что выполняется равенство:
$\frac{AP}{PB} \cdot \frac{BQ}{QC} \cdot \frac{CR}{RA} = 1$
Перемножим полученные нами выражения:
$(\frac{A_1A}{OA_1} \cdot \frac{B_1O}{BB_1}) \cdot (\frac{B_1B}{OB_1} \cdot \frac{C_1O}{CC_1}) \cdot (\frac{C_1C}{OC_1} \cdot \frac{A_1O}{AA_1}) = $
$= \frac{AA_1}{OA_1} \cdot \frac{OB_1}{BB_1} \cdot \frac{BB_1}{OB_1} \cdot \frac{OC_1}{CC_1} \cdot \frac{CC_1}{OC_1} \cdot \frac{OA_1}{AA_1} = 1$
(Мы использовали равенства $A_1A=AA_1$, $B_1O=OB_1$ и т.д., так как речь идет об отношениях длин отрезков).Так как произведение отношений равно 1, по обратной теореме Менелая точки $P, Q, R$ лежат на одной прямой.
Случай 2: Прямые $AA_1, BB_1, CC_1$ попарно параллельны.
Пусть $\vec{u}$ - направляющий вектор этих параллельных прямых. Выберем произвольное начало отсчета. Тогда положение вершин можно описать векторными равенствами:
$\vec{A_1} = \vec{A} + k_A \vec{u}$, $\vec{B_1} = \vec{B} + k_B \vec{u}$, $\vec{C_1} = \vec{C} + k_C \vec{u}$
Точка $P$ лежит на прямой $AB$, поэтому ее радиус-вектор $\vec{P} = (1-t)\vec{A} + t\vec{B}$.Точка $P$ также лежит на прямой $A_1B_1$, поэтому $\vec{P} = (1-s)\vec{A_1} + s\vec{B_1}$.Подставим выражения для $\vec{A_1}$ и $\vec{B_1}$:
$\vec{P} = (1-s)(\vec{A} + k_A \vec{u}) + s(\vec{B} + k_B \vec{u}) = (1-s)\vec{A} + s\vec{B} + ((1-s)k_A + sk_B)\vec{u}$
Так как точка $P$ лежит в плоскости $\triangle ABC$, а вектор $\vec{u}$ (в общем случае) не компланарен этой плоскости, коэффициент при $\vec{u}$ должен быть равен нулю:
$(1-s)k_A + sk_B = 0 \implies k_A - sk_A + sk_B = 0 \implies s = \frac{k_A}{k_A-k_B}$
При этом $(1-t)\vec{A} + t\vec{B} = (1-s)\vec{A} + s\vec{B}$, откуда $t=s$.Подставив $s$ в выражение для $\vec{P}$, получаем:
$\vec{P} = (1 - \frac{k_A}{k_A-k_B})\vec{A} + \frac{k_A}{k_A-k_B}\vec{B} = \frac{-k_B\vec{A} + k_A\vec{B}}{k_A-k_B}$
Поступая аналогично для точек $Q$ и $R$, получаем:
$\vec{Q} = \frac{-k_C\vec{B} + k_B\vec{C}}{k_B-k_C}$
$\vec{R} = \frac{-k_A\vec{C} + k_C\vec{A}}{k_C-k_A}$
Чтобы проверить, что точки $P, Q, R$ коллинеарны, достаточно показать, что их радиус-векторы линейно зависимы, причем сумма коэффициентов равна нулю. Рассмотрим комбинацию:
$(k_A-k_B)\vec{P} + (k_B-k_C)\vec{Q} + (k_C-k_A)\vec{R}$
Сумма коэффициентов $(k_A-k_B) + (k_B-k_C) + (k_C-k_A) = 0$.Подставим выражения для векторов:
$(-k_B\vec{A} + k_A\vec{B}) + (-k_C\vec{B} + k_B\vec{C}) + (-k_A\vec{C} + k_C\vec{A}) = $
$= \vec{A}(-k_B+k_C) + \vec{B}(k_A-k_C) + \vec{C}(k_B-k_A) = (k_C-k_B)\vec{A} + (k_A-k_C)\vec{B} + (k_B-k_A)\vec{C}$
Сумма коэффициентов при $\vec{A}, \vec{B}, \vec{C}$ также равна нулю: $(k_C-k_B) + (k_A-k_C) + (k_B-k_A) = 0$. Это означает, что точки $P, Q, R$ лежат на одной прямой.
Ответ: Доказано, что если прямые $AA_1, BB_1, CC_1$ пересекаются в одной точке или параллельны, то точки $P, Q, R$ лежат на одной прямой.
Доказательство достаточности (Условие 2 $\implies$ Условие 1)
Предположим, что точки $P, Q, R$ лежат на одной прямой $l$. Нам нужно доказать, что прямые $AA_1, BB_1, CC_1$ пересекаются в одной точке или параллельны. Мы докажем это методом от противного, используя уже доказанную первую часть теоремы.
Случай 1: Две из прямых, например $AA_1$ и $BB_1$, пересекаются в точке $O$.
Предположим, что прямая $CC_1$ не проходит через точку $O$.Рассмотрим прямую $OC$. Она пересечет прямую $A_1C_1$ в некоторой точке. Она также пересечет прямую $B_1C_1$ в некоторой точке. Давайте определим новую точку $C_2$ на прямой $OC$ так, чтобы построить новый треугольник, для которого можно применить первую часть теоремы.
Пусть $C_2$ — точка пересечения прямых $OC$ и $A_1C_1$. Это неверный подход. Правильный подход:
Пусть прямая $OC$ пересекает прямую $B_1C_1$ в точке $C_2'$. Это тоже сложно. Проще всего так: Пусть $AA_1 \cap BB_1 = O$. Рассмотрим треугольники $ABC$ и $A_1B_1C_1$. Предположим, что $CC_1$ не проходит через $O$.Построим точку $C_2$ на прямой $OC$ так, что $C_2$ лежит на прямой $A_1B_1$. Это неверно.
Правильная конструкция: Пусть $C_2$ — точка на прямой $OC$ (т.е. $O, C, C_2$ коллинеарны).Рассмотрим треугольники $ABC$ и $A_1B_1C_2$. По построению, прямые, соединяющие их соответственные вершины ($AA_1, BB_1, CC_2$), пересекаются в точке $O$.Следовательно, по доказанной первой части теоремы, точки пересечения их соответственных сторон должны лежать на одной прямой. Найдем эти точки:
- $AB \cap A_1B_1 = P$
- $BC \cap B_1C_2 = Q'$
- $CA \cap C_2A_1 = R'$
Таким образом, точки $P, Q', R'$ лежат на одной прямой.
По условию нашей теоремы, точки $P, Q, R$ также лежат на одной прямой $l$.Поскольку точка $P$ общая для обеих троек коллинеарных точек, то обе тройки лежат на одной и той же прямой $l$. Значит, $Q'$ и $R'$ также лежат на прямой $l$.
Рассмотрим точку $Q'$. Она лежит на прямой $BC$ (по определению) и на прямой $l$. Точка $Q$ также лежит на прямой $BC$ (по определению) и на прямой $l$. Если прямая $BC$ и $l$ не совпадают (невырожденный случай), то $Q' = Q$.$Q = BC \cap B_1C_1$ (по условию).$Q' = BC \cap B_1C_2$ (по построению).Так как $Q = Q'$, точка $Q$ лежит на обеих прямых $B_1C_1$ и $B_1C_2$. Поскольку точка $B_1$ также принадлежит обеим прямым, эти прямые совпадают. Следовательно, точка $C_2$ лежит на прямой $B_1C_1$.
Аналогично, $R' = R$. Точка $R$ лежит на прямой $CA$ и $l$. Точка $R'$ также лежит на $CA$ и $l$. Значит $R=R'$.$R = CA \cap C_1A_1$ (по условию).$R' = CA \cap C_2A_1$ (по построению).Из $R = R'$ следует, что точка $R$ лежит на обеих прямых $C_1A_1$ и $C_2A_1$. Поскольку $A_1$ также на обеих, прямые совпадают. Значит, точка $C_2$ лежит на прямой $C_1A_1$.
Итак, мы показали, что $C_2$ лежит на $B_1C_1$ и на $C_1A_1$. Единственная общая точка этих двух прямых — это $C_1$. Таким образом, $C_2 = C_1$.Но мы строили $C_2$ на прямой $OC$. Следовательно, $C_1$ лежит на прямой $OC$, то есть прямая $CC_1$ проходит через точку $O$. Это противоречит нашему предположению. Значит, если $AA_1$ и $BB_1$ пересекаются в точке $O$, то и $CC_1$ проходит через $O$.
Случай 2: Две из прямых, например $AA_1$ и $BB_1$, параллельны.
Докажем, что $CC_1$ им параллельна. Предположим противное: $CC_1$ не параллельна $AA_1$.Построим прямую, проходящую через $C$ параллельно $AA_1$, и на ней точку $C_2$ (это можно сделать, задав $\vec{C_2} = \vec{C} + k \vec{u}$, где $\vec{u}$ - направляющий вектор $AA_1$).Теперь рассмотрим треугольники $ABC$ и $A_1B_1C_2$. Прямые, соединяющие их соответственные вершины ($AA_1, BB_1, CC_2$), по построению параллельны. По доказанной первой части теоремы (для параллельного случая), точки пересечения их соответственных сторон лежат на одной прямой.
- $AB \cap A_1B_1 = P$
- $BC \cap B_1C_2 = Q''$
- $CA \cap C_2A_1 = R''$
Значит, точки $P, Q'', R''$ коллинеарны. Дальнейшие рассуждения полностью аналогичны предыдущему случаю. Из коллинеарности $P,Q,R$ и $P,Q'',R''$ следует, что $Q=Q''$ и $R=R''$. Из этого, в свою очередь, следует, что $C_2=C_1$. А так как прямая $CC_2$ была построена параллельно $AA_1$, то и прямая $CC_1$ параллельна $AA_1$. Это противоречит предположению.
Таким образом, оба случая приводят к выводу, что прямые $AA_1, BB_1, CC_1$ либо пересекаются в одной точке, либо попарно параллельны.
Ответ: Доказано, что если точки $P, Q, R$ лежат на одной прямой, то прямые $AA_1, BB_1, CC_1$ пересекаются в одной точке или попарно параллельны.
Другие задания:
Помогло решение? Оставьте отзыв в комментариях ниже.
Присоединяйтесь к Телеграм-группе @top_gdz
ПрисоединитьсяМы подготовили для вас ответ c подробным объяснением домашего задания по геометрии за 10-11 класс, для упражнения номер 858 расположенного на странице 219 к учебнику 2019 года издания для учащихся школ и гимназий.
Теперь на нашем сайте ГДЗ.ТОП вы всегда легко и бесплатно найдёте условие с правильным ответом на вопрос «Как решить ДЗ» и «Как сделать» задание по геометрии к упражнению №858 (с. 219), авторов: Атанасян (Левон Сергеевич), Бутузов (Валентин Фёдорович), Кадомцев (Сергей Борисович), Позняк (Эдуард Генрихович), Киселёва (Людмила Сергеевна), ФГОС (старый) базовый и углублённый уровень обучения учебного пособия издательства Просвещение.




















